Batch 3 - Class 159 - Eulerian and Planar Graphs, Topology
Attendance Muskaan, Arnav, Anishka, Liza, Siddhanth, Aashvi, Anshi
Class puzzles
Coloring a Doodle (Eulerian graphs)
A kid is bored of the classes so she starts to doodle. While doodling, she follows some simple rules:
- Once started, she doesn't lift the pen off the paper
- She finishes at the exact point she started
- She is unable to retrace her steps back over a piece of curve already drawn
The result is a curve with several self intersections, like this
.png)
Now she starts color this doodle to make regions black and others white, so that no regions sharing a border are of the same color. Lands up with the following:

Can the above be done with any other such doodle? Or are there cases where you would have to leave two regions with common border with the same color?
Can you prove it?
Homes and Utilities (Planar Graphs)
There are three homes and three utilities that must be supplied to each of the three homes, as under:
.png)
Can you connect each of the three utilities to each of the three houses, so that none of the pipelines cross?
Is there another way of placing the three houses and location of three utilities to make it happen?
If not, what is the least number of intersections you need to make it happen?
- Answer: You can do it with one intersection
.png)
If these were not on a flat surface, but on another kind of surface could you do it?
- Answer: Yes, it can be done on a torus
.png)
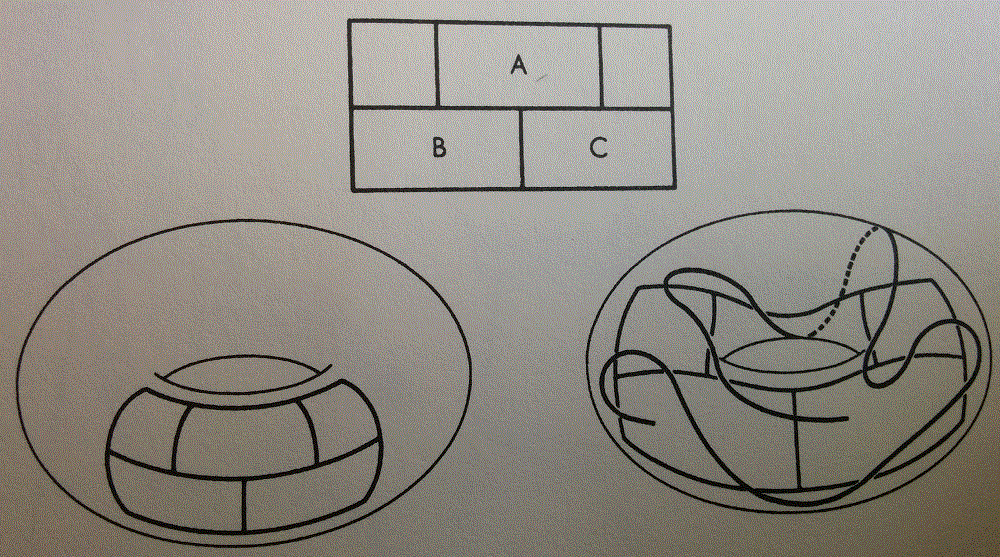
- MartinShCol 8.7 - See figure below and draw a line which intersects each of the 16 segments exactly once
- Answer: Can not be done because each of A, B, C have 5 sides each so a line can't enter and leave (even points of intersection) - note that two of these could be start and end points
- Can you do it on a Torus (Introduce the torus to kids)
- Yes, by having one point of entry "under" the drawing! (See bottom right solution)
Homework Problem:
- In the problem above, can you attempt to find a surface where the loop can be closed?
References:
The Colossal Book of Short Puzzles and Problems, by Martin Gardner